
This table compares the effective key strength of symmetric cryptography, integer-based public key cryptography, and ECC. The first of these is key length, as demonstrated in the table below. That said, ECC has a couple of advantages over integer-based public key cryptography. This means that ECC algorithms will also be breakable when quantum computing makes Shor’s Algorithm usable. Why use ECC?ĮCC is based on the same “hard” problems as classical integer-based public key cryptography. Using this relationship, it is possible to build Diffie-Hellman using elliptic curves. Since point division is equivalent to logarithms, it’s a “hard” problem, making it infeasible to learn a from aX. With elliptic curve cryptography, x a becomes aX, where X is a point on the elliptic curve. have complexity that is exponentially related to the length of the exponents), Diffie-Hellman users can publicly exchange x a and x b without fearing that an eavesdropper could learn the values of their private keys a and b. Due to the fact that logarithms are “hard” (i.e.

Key exchange is based on the fact that (x a ) b =(x b ) a =x ab. This means that it is possible to slightly tweak existing cryptographic algorithms to work with points on an elliptic curve.įor example, Diffie-Hellman is all about exponentiation. These operations are the same operations used to build classical, integer-based asymmetric cryptography.
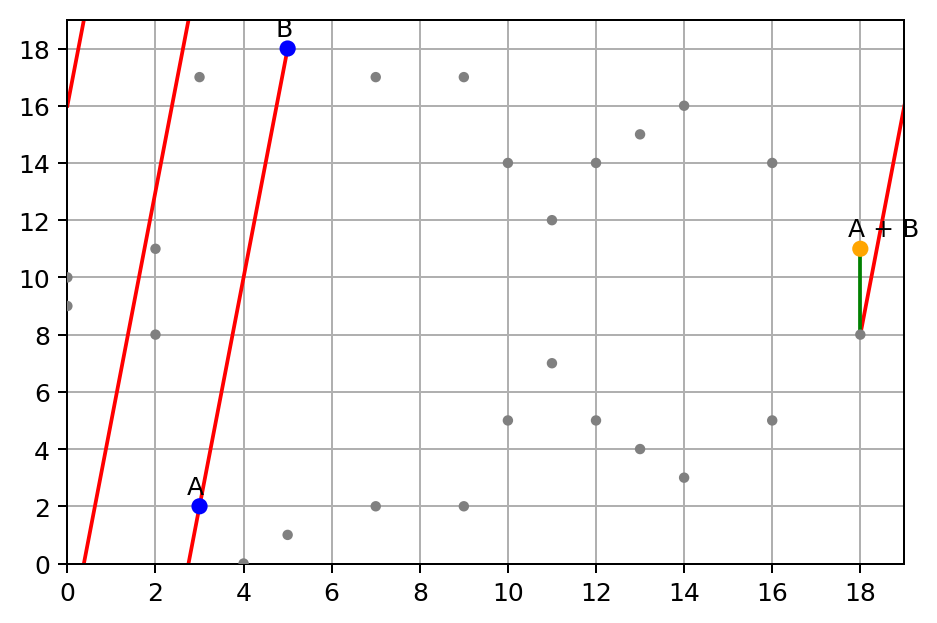
Multiplying two points on an elliptic curve is equivalent to exponentiation.Adding two points on an elliptic curve is equivalent to multiplication.The problems used in classical asymmetric cryptography are the discrete logarithm problem (exponents are easy, logarithms are hard) and the factoring problem (multiplication is easy, factoring is hard).Įlliptic curve cryptography is based on the fact that certain mathematical operations on elliptic curves are equivalent to mathematical functions on integers: These are mathematical functions that are easy to perform but difficult to reverse. Public key cryptography is based on mathematically “hard” problems.


 0 kommentar(er)
0 kommentar(er)
